Almudena Rueda. EcosimPro Applications Team
One of the ways to simulate a system is by implementing and solving the equations that govern its behaviour. This is precisely what allows EcosimPro/PROOSIS to represent a process by means of algebraic differential equations and any potential events that could appear.
EcosimPro/PROOSIS can then be viewed as a pure solver of a series of previously-defined equations. There is a possibility that, when the equations are ordered, a set of them cannot be solved explicitly and need to be solved simultaneously. In turn, these equation systems can be linear or non-linear.
Whenever the equation system is linear, the problem is transparent to the user, that is, EcosimPro/PROOSIS has a solver that can solve the box without asking the user.
However, in non-linear equation systems EcosimPro/PROOSIS uses a particular heuristic technique based on the classical Equation Tearing algorithm. It identifies a set of variables on which the iteration is based to solve the non-linear box (tearing variables).
These non-linear boxes are common in models where only algebraic equations are used (steady simulation tools that are typical in engineering design and analysis)
The tearing variables and the residue equations need to be adequately selected to ensure the robust resolution of the non-linear equation systems. The aspects that a simulation engineer needs to take into account for this choice are following:
- the difficulty in solving certain equations: thus, for instance, equations where the tearing variable is dividing can create problems of divisions by zero. Selecting it would therefore not be appropriate.
- the correct behaviour of the physics of the problem will always help to improve the selection.
A good choice of tearing variables and implicit equations has a direct bearing on the convergence properties of our model, hence its importance.
Normally a good choice is done automatically by EcosimPro/PROOSIS through the Equation Tearing algorithm. However, the modeller has a chance to modify it and improve it.
However, even better than the capability of changing this selection is possibility of ‘aiming’ the algorithm towards the solution we consider the most appropriate. This is done by means of the EL language (EcosimPro/PROOSIS language). The modeller can use certain directives to impose what variables are going to be tearing variables and what equations are going to be selected as implicit or closure equations so that it is easier to solve non-linear equation systems.
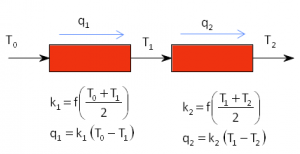
The following system can be used as a basis to explain how to obtain non-linear boxes that are more robust from the point of view of convergence:
The implementation in EcosimPro/PROOSIS would be as follows:
These are two heat ducts in serial connection where the inlet and outlet temperatures are known (T0 and T2 respectively), and where the conductivity depends on the temperature.
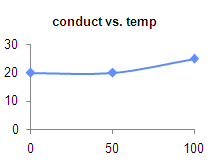
The graph shows that conductivity remains constant up to 50ºC, so the modeller needs to realise that temperature changes do not have a bearing on conductivity.
The previous model has a non-linear box because the conductivity depends on the temperature at the ends of each duct. EcosimPro/PROOSIS suggests the following when it applies Equation Tearing to solve this box:
- tearing variable: T1
- residue equation: cond2 = linearInterp1D(cond_vs_Tave, 0.5 * (T1 + T2))
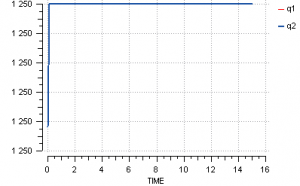
When the simulation is run, the solver fails because the equation that was selected as implicit or closure equation is not sensitive to changes in the tearing variable.
When the physics of the problem are analysed it is easy to determine that the correct choice would have been the following:
- tearing variable: T1
- implicit equation: 0 = q1 – cond2 * (T1 – T2)
How can this be achieved? New directives need to be introduced in the modelling. Below are some possible solutions.
Solution 1: EXPL directive
If a variable is declared as EXPL, it will be calculated explicitly by means of the corresponding equation. If this system is applied to the above system, the conductivities will be calculated directly with the table. The simulation is then run correctly.
Solution 2: SEQUENTIAL block
Sequential blocks in EcosimPro/PROOSIS are run sequentially. The process is therefore similar to running a function. If the calculation of the conductivity is done in this way, we will therefore avoid the possibility of selecting these equations as implicit equations, so that the required non-linear box will be obtained.
Solution 3: IMPL (tearing variable) directive
Finally, the IMPL(variable) operator can be used. This operator ‘sets’ the equation that is to be implicit and the tearing variable at the same time. The following is obtained when it is applied to our case:
Again, using these operators has yielded a robust system of non-linear equations. The system simulation will therefore not have any convergence problems.
As a conclusion, it can be stated that the modeller should program the components to be as robust as possible so that the algebraic variables that are selected and the residue equations will be robust to allow convergence.
EcosimPro/PROOSIS currently selects automatically a set of algebraic equations/residue equations to be selected that in many cases is good enough, but the upcoming versions will go even further and help minimise the number of algebraic equations and detect convergence problems with the residue before any study is done. This will allow more robust mathematical problems to be created and typical problems in these cases, such as non-convergence, to be predicted.